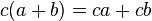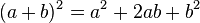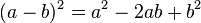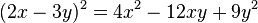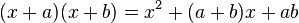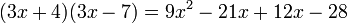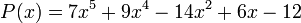SUMA DE VECTORES
La suma de vectores A y B se obtiene al hacer coincidir el extremo de uno de ellos con el origen del otro; la suma es el vector que va del inicio del primero al extremo del segundo.
Las propiedades de la suma de vectores son:
Propiedad conmutativa
Propiedad de la desigualdad del triángulo
Propiedad asociativa
La suma de vectores se puede realizar de dos formas, la primera es utilizando la ley de los senos y cosenos, la segunda forma es por medio de descomposición de fuerzas. Más adelante hay varios problemas aplicando lo antes dicho.
RESTA DE VECTORES.
Restar el vector B del vector A es equivalente a sumarle el inverso aditivo de B. Para restar vectores se unen en su origen y el vector resta es la unión de sus extremos dibujando el sentido hacia el que se le va a quitar, el paso siguiente es calcular el vector con el mismo procedimiento que en la suma.
RESTA DE VECTORES.
Restar el vector B del vector A es equivalente a sumarle el inverso aditivo de B. Para restar vectores se unen en su origen y el vector resta es la unión de sus extremos dibujando el sentido hacia el que se le va a quitar, el paso siguiente es calcular el vector con el mismo procedimiento que en la suma.
miércoles, 22 de junio de 2011
Como lo podemos Graficar,Analiticamente,,Graficamente
•
Representación grafica de un vector. Dado su origen y su extremo.
C Origen d. Extremo c. Dirección vertical con sentido hacia arriba. Se denota d c
D
Origen f. Extremo e. Dirección inclinada hacia la derecha con sentido ascendente. Se denota f e
E
F
•
Componentes de un vector grafica y analíticamente. Con ejemplos.
Se llama componentes de un vector, situado ene un sistema de coordenadas, al punto que tiene como abcisas la diferencia de las abcisas y como ordenada la diferencia de las ordenadas de los puntos que conforman el extremo y el origen, en ese orden.
•
analíticamente:
dados los puntos a (3,4) b (-2,3) c (-4,-3) y d (1,0). Determinar las componentes de cada uno delos siguientes vectores: a) ab b) bc c) cd.
a) ab a (3,4) b (-2,). b-a
Abcisas -2-3 = -5
Ordenadas 3-4 = -1
Representación grafica de un vector. Dado su origen y su extremo.
C Origen d. Extremo c. Dirección vertical con sentido hacia arriba. Se denota d c
D
Origen f. Extremo e. Dirección inclinada hacia la derecha con sentido ascendente. Se denota f e
E
F
•
Componentes de un vector grafica y analíticamente. Con ejemplos.
Se llama componentes de un vector, situado ene un sistema de coordenadas, al punto que tiene como abcisas la diferencia de las abcisas y como ordenada la diferencia de las ordenadas de los puntos que conforman el extremo y el origen, en ese orden.
•
analíticamente:
dados los puntos a (3,4) b (-2,3) c (-4,-3) y d (1,0). Determinar las componentes de cada uno delos siguientes vectores: a) ab b) bc c) cd.
a) ab a (3,4) b (-2,). b-a
Abcisas -2-3 = -5
Ordenadas 3-4 = -1
Elementos del vectOr!!
◦
La Dirección: esta determinada por la recta de soporte y puede ser vertical, horizontal e inclinada u oblicua.
◦
La orientación: o sentido, esta determinada por la flecha y puede ser horizontal hacia la derecha o hacia la izquierda, vertical hacia arriba o hacia abajo e inclinada ascendente o descendente hacia la derecha o hacia la izquierda.
◦
El punto de aplicación: esta determinado por el punto origen del segmento que forma el vector.
◦
La longitud o módulo: es el número positivo que representa la longitud del vector.
La Dirección: esta determinada por la recta de soporte y puede ser vertical, horizontal e inclinada u oblicua.
◦
La orientación: o sentido, esta determinada por la flecha y puede ser horizontal hacia la derecha o hacia la izquierda, vertical hacia arriba o hacia abajo e inclinada ascendente o descendente hacia la derecha o hacia la izquierda.
◦
El punto de aplicación: esta determinado por el punto origen del segmento que forma el vector.
◦
La longitud o módulo: es el número positivo que representa la longitud del vector.
Que es un vector??
El estudio de los vectores es uno de tantos conocimientos de las matemáticas que provienen de la física. En esta ciencia se distingue entre magnitudes escalares y magnitudes vectoriales. Se llaman magnitudes escalares aquellas en que sólo influye su tamaño. Por el contrario, se consideran magnitudes vectoriales aquellas en las que, de alguna manera, influyen la dirección y el sentido en que se aplican.
Como ejemplos de magnitudes escalares se pueden citar la masa de un cuerpo, la temperatura, el volumen, etc.
Cuando se plantea un movimiento no basta con decir cuánto se ha desplazado el móvil, sino que es preciso decir también en qué dirección y sentido ha tenido lugar el movimiento. No son los mismos los efectos de un movimiento de 100 km a partir de un punto si se hace hacia el norte o si se hace en dirección sudoeste, ya que se llegaría a distinto lugar.
Aunque el estudio matemático de los vectores tardó mucho en hacerse formalmente, en la actualidad tiene un gran interés, sobre todo a partir de los estudios de David Hilbert (1862-1943) y Stefan Banach (1892-1945), que hicieron uso de la teoría de espacios vectoriales, aplicándolos a las técnicas del análisis matemático.
Por lo tanto el resultado de nuestra investigación esta enmarcada en los concepto, graficas y ejercicio que a continuación le expondremos.
•
Definición de Vectores.
En matemáticas, cantidad que tiene magnitud, dirección y sentido al mismo tiempo. Por ejemplo, si una cantidad ordinaria, o escalar, puede ser una distancia de 6 km, una cantidad vectorial sería decir 6 km norte. Los vectores se representan normalmente como segmentos rectilíneos orientados, como B en el diagrama que se muestra a continuación; el punto O es el origen o punto de aplicación del vector y B su extremo. La longitud del segmento es la medida o módulo de la cantidad vectorial, y su dirección es la misma que la del vector.
El uso sencillo de los vectores así como los cálculos utilizando vectores quedan ilustrados en este diagrama, que muestra el movimiento de una barca para atravesar una corriente de agua. El vector a, u A, indica el movimiento de la barca durante un determinado periodo de tiempo si estuviera navegando en aguas tranquilas; el vector b, o $, representa la deriva o empuje de la corriente durante el mismo periodo de tiempo. El recorrido real de la barca, bajo la influencia de su propia propulsión y de la corriente, se representa con el vector c, u B. Utilizando vectores, se puede resolver gráficamente cualquier problema relacionado con el movimiento de un objeto bajo la influencia de varias fuerzas.
Como ejemplos de magnitudes escalares se pueden citar la masa de un cuerpo, la temperatura, el volumen, etc.
Cuando se plantea un movimiento no basta con decir cuánto se ha desplazado el móvil, sino que es preciso decir también en qué dirección y sentido ha tenido lugar el movimiento. No son los mismos los efectos de un movimiento de 100 km a partir de un punto si se hace hacia el norte o si se hace en dirección sudoeste, ya que se llegaría a distinto lugar.
Aunque el estudio matemático de los vectores tardó mucho en hacerse formalmente, en la actualidad tiene un gran interés, sobre todo a partir de los estudios de David Hilbert (1862-1943) y Stefan Banach (1892-1945), que hicieron uso de la teoría de espacios vectoriales, aplicándolos a las técnicas del análisis matemático.
Por lo tanto el resultado de nuestra investigación esta enmarcada en los concepto, graficas y ejercicio que a continuación le expondremos.
•
Definición de Vectores.
En matemáticas, cantidad que tiene magnitud, dirección y sentido al mismo tiempo. Por ejemplo, si una cantidad ordinaria, o escalar, puede ser una distancia de 6 km, una cantidad vectorial sería decir 6 km norte. Los vectores se representan normalmente como segmentos rectilíneos orientados, como B en el diagrama que se muestra a continuación; el punto O es el origen o punto de aplicación del vector y B su extremo. La longitud del segmento es la medida o módulo de la cantidad vectorial, y su dirección es la misma que la del vector.
El uso sencillo de los vectores así como los cálculos utilizando vectores quedan ilustrados en este diagrama, que muestra el movimiento de una barca para atravesar una corriente de agua. El vector a, u A, indica el movimiento de la barca durante un determinado periodo de tiempo si estuviera navegando en aguas tranquilas; el vector b, o $, representa la deriva o empuje de la corriente durante el mismo periodo de tiempo. El recorrido real de la barca, bajo la influencia de su propia propulsión y de la corriente, se representa con el vector c, u B. Utilizando vectores, se puede resolver gráficamente cualquier problema relacionado con el movimiento de un objeto bajo la influencia de varias fuerzas.
martes, 5 de abril de 2011
viernes, 1 de abril de 2011
Rincon Patrio
Simon Bolivar
Simón José Antonio de la Santísima Trinidad Bolívar y Palacios de Aguirre, Ponte-Andrade y Blanco, mejor conocido como Simón Bolívar, (Caracas, 24 de julio[2] de 1783 — Santa Marta, República de Nueva Granada, 17 de diciembre de 1830) fue un militar y político venezolano de la época pre-republicana de la Capitanía General de Venezuela; fundador de la Gran Colombia y una de las figuras más destacadas de la Emancipación Americana frente al Imperio español. Contribuyó de manera decisiva a la independencia de las actuales Bolivia, Colombia, Ecuador, Panamá, Perú y Venezuela.
Le fue concedido el título honorífico de Libertador por el Cabildo de Mérida en Venezuela que, tras serle ratificado en Caracas, quedó asociado a su nombre. Los problemas para llevar adelante sus planes fueron tan frecuentes que llegó a afirmar de sí mismo que era "el hombre de las dificultades" en una carta dirigida al general Francisco de Paula Santander en 1825.
Participó en la fundación de la Gran Colombia, nación que intentó consolidar como una gran confederación política y militar en América, de la cual fue Presidente. Bolívar es considerado por sus acciones e ideas el "Hombre de América" y una destacada figura de la Historia Universal, ya que dejó un legado político en diversos países latinoamericanos, algunos de los cuales le han convertido en objeto de veneración nacionalista. Ha recibido honores en varias partes del mundo a través de estatuas o monumentos, parques, plazas, etc.
Infancia
Las referencias que dejó Bolívar en su correspondencia hacen suponer que su infancia fue dichosa, feliz, segura, rodeada de sólidos afectos y gratos recuerdos con parientes destacados e influyentes dentro de un ambiente aristocrático y en general, dentro de un ambiente que le brindó equilibrio emocional, cariño y afecto.
En este sentido existen algunas anécdotas que se popularizaron en Venezuela que presentaban a Bolívar como un niño turbulento debido a que los escritores románticos consideraron indispensable atribuirle una niñez indómita creyendo, según la moda de la época, que no podía salir un hombre excepcional de un niño normal pero se ha demostrado que esas anécdotas fueron inventadas e introducidas en los relatos de Historia por Arístides Rojas, considerado un excelente narrador pero que usó a menudo su imaginación a falta de documentos que demostraran la veracidad de sus relatos.
Simón, de la estirpe vasca de los Bolibarjauregui, pero de raza tirando a mulata, nació en la noche del 24 al 25 de julio[4] de 1783 en una casa solariega ubicada en la Plaza San Jacinto de Caracas.[5] Fue bautizado el 30 de julio de 1783, en la Catedral de Caracas, con los nombres de Simón José Antonio de la Santísima Trinidad de la Concepción, por el doctor Juan Félix Jerez Aristeguieta, su primo hermano quien, de acuerdo con don Juan Vicente, padre del niño, le puso el nombre de Simón.
En enero de 1786, cuando Simón contaba dos años de edad, su padre murió de tuberculosis, y así doña Concepción quedó como cabeza de familia, velando eficientemente por los intereses de la familia hasta su muerte.
Infancia
El desempeño escolar de Bolívar no fue muy brillante como alumno de la Escuela Pública, institución administrada por el Cabildo de Caracas que funcionaba de forma deficiente debido a la carencia de recursos y organización.
Al poco tiempo, Rodríguez renunció a su cargo de maestro para irse a Europa y la Real Audiencia de Caracas determinó que Simón fuera trasladado a la Academia de Matemáticas, dirigida por el padre Andújar y que funcionaba en casa de su tío Carlos.
Al parecer, en esta academia la formación de Bolívar mejoró notablemente en calidad y cantidad, y fue complementada con lecciones de Historia y Cosmografía impartidas por don Andrés Bello hasta su ingreso en el Batallón de Milicias de blancos de los Valles de Aragua el 14 de enero de 1797.
Existe la falsa idea de que entre 1793 y 1795, está inscrito al Colegio Real de Sorèze en el Sur de Francia, en el departamento del Tarn.[
Simón José Antonio de la Santísima Trinidad Bolívar y Palacios de Aguirre, Ponte-Andrade y Blanco, mejor conocido como Simón Bolívar, (Caracas, 24 de julio[2] de 1783 — Santa Marta, República de Nueva Granada, 17 de diciembre de 1830) fue un militar y político venezolano de la época pre-republicana de la Capitanía General de Venezuela; fundador de la Gran Colombia y una de las figuras más destacadas de la Emancipación Americana frente al Imperio español. Contribuyó de manera decisiva a la independencia de las actuales Bolivia, Colombia, Ecuador, Panamá, Perú y Venezuela.
Le fue concedido el título honorífico de Libertador por el Cabildo de Mérida en Venezuela que, tras serle ratificado en Caracas, quedó asociado a su nombre. Los problemas para llevar adelante sus planes fueron tan frecuentes que llegó a afirmar de sí mismo que era "el hombre de las dificultades" en una carta dirigida al general Francisco de Paula Santander en 1825.
Participó en la fundación de la Gran Colombia, nación que intentó consolidar como una gran confederación política y militar en América, de la cual fue Presidente. Bolívar es considerado por sus acciones e ideas el "Hombre de América" y una destacada figura de la Historia Universal, ya que dejó un legado político en diversos países latinoamericanos, algunos de los cuales le han convertido en objeto de veneración nacionalista. Ha recibido honores en varias partes del mundo a través de estatuas o monumentos, parques, plazas, etc.
Infancia
Las referencias que dejó Bolívar en su correspondencia hacen suponer que su infancia fue dichosa, feliz, segura, rodeada de sólidos afectos y gratos recuerdos con parientes destacados e influyentes dentro de un ambiente aristocrático y en general, dentro de un ambiente que le brindó equilibrio emocional, cariño y afecto.
En este sentido existen algunas anécdotas que se popularizaron en Venezuela que presentaban a Bolívar como un niño turbulento debido a que los escritores románticos consideraron indispensable atribuirle una niñez indómita creyendo, según la moda de la época, que no podía salir un hombre excepcional de un niño normal pero se ha demostrado que esas anécdotas fueron inventadas e introducidas en los relatos de Historia por Arístides Rojas, considerado un excelente narrador pero que usó a menudo su imaginación a falta de documentos que demostraran la veracidad de sus relatos.
Simón, de la estirpe vasca de los Bolibarjauregui, pero de raza tirando a mulata, nació en la noche del 24 al 25 de julio[4] de 1783 en una casa solariega ubicada en la Plaza San Jacinto de Caracas.[5] Fue bautizado el 30 de julio de 1783, en la Catedral de Caracas, con los nombres de Simón José Antonio de la Santísima Trinidad de la Concepción, por el doctor Juan Félix Jerez Aristeguieta, su primo hermano quien, de acuerdo con don Juan Vicente, padre del niño, le puso el nombre de Simón.
En enero de 1786, cuando Simón contaba dos años de edad, su padre murió de tuberculosis, y así doña Concepción quedó como cabeza de familia, velando eficientemente por los intereses de la familia hasta su muerte.
Infancia
El desempeño escolar de Bolívar no fue muy brillante como alumno de la Escuela Pública, institución administrada por el Cabildo de Caracas que funcionaba de forma deficiente debido a la carencia de recursos y organización.
Al poco tiempo, Rodríguez renunció a su cargo de maestro para irse a Europa y la Real Audiencia de Caracas determinó que Simón fuera trasladado a la Academia de Matemáticas, dirigida por el padre Andújar y que funcionaba en casa de su tío Carlos.
Al parecer, en esta academia la formación de Bolívar mejoró notablemente en calidad y cantidad, y fue complementada con lecciones de Historia y Cosmografía impartidas por don Andrés Bello hasta su ingreso en el Batallón de Milicias de blancos de los Valles de Aragua el 14 de enero de 1797.
Existe la falsa idea de que entre 1793 y 1795, está inscrito al Colegio Real de Sorèze en el Sur de Francia, en el departamento del Tarn.[
miércoles, 30 de marzo de 2011
Productos Notables
Productos notables es el nombre que reciben aquellas multiplicaciones con expresiones algebraicas cuyo resultado puede ser escrito por simple inspección, sin verificar la multiplicación que cumplen ciertas reglas fijas. Su aplicación simplifica y sistematiza la resolución de muchas multiplicaciones habituales.
.
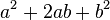, se conoce como trinomio cuadrado perfecto.
Cuando el segundo término es negativo, la ecuación que se obtiene es:
Dos binomios conjugados son aquellos que sólo se diferencien en el signo de la operación. Para multiplicar binomios conjugados, basta elevar los monomios al cuadrado y restarlos, obteniendo una diferencia de cuadrados
Productos notables es el nombre que reciben aquellas multiplicaciones con expresiones algebraicas cuyo resultado puede ser escrito por simple inspección, sin verificar la multiplicación que cumplen ciertas reglas fijas. Su aplicación simplifica y sistematiza la resolución de muchas multiplicaciones habituales.
.
Factor común
El resultado de multiplicar un binomio a+b con un término c se obtiene aplicando la propiedad distributiva: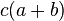
(el producto de la base por la altura), que también puede obtenerse como la suma de las dos áreas coloreadas (ca) y (cb).
- Ejemplo
Binomio al cuadrado o cuadrado de un binomio
Para elevar un binomio al cuadrado (es decir, multiplicarlo por sí mismo), se suman los cuadrados de cada término con el doble del producto de ellos. Es decir: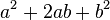
, se conoce como trinomio cuadrado perfecto.Cuando el segundo término es negativo, la ecuación que se obtiene es:
- Ejemplo
Producto de dos binomios con un término común
Cuando se multiplican dos binomios que tienen un término común, se suma el cuadrado del término común con el producto el término común por la suma de los otros, y al resultado se añade el producto de los términos diferentes.
- Ejemplo
Producto de dos binomios conjugados
Dos binomios conjugados son aquellos que sólo se diferencien en el signo de la operación. Para multiplicar binomios conjugados, basta elevar los monomios al cuadrado y restarlos, obteniendo una diferencia de cuadrados
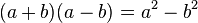
- Ejemplo
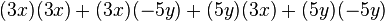
agrupando términos:
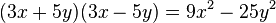
A este producto notable también se le conoce como suma por la diferencia
Polinomio al cuadrado
Para elevar un polinomio con cualquier cantidad de términos, se suman los cuadrados de cada término individual y luego se añade el doble de la suma de los productos de cada posible par de términos.
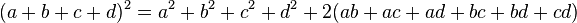
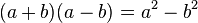
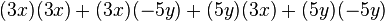
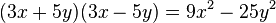
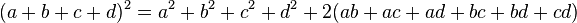
Factorizacion
En álgebra, la factorización es expresar un objeto o número (por ejemplo, un número compuesto, una matriz o un polinomio) como producto de otros objetos más pequeños (factores), (en el caso de números debemos utilizar los números primos) que, al multiplicarlos todos, resulta el objeto original. Por ejemplo, el número 15 se factoriza en números primos 3 × 5; y a²-b² se factoriza como binomio conjugados (a - b)(a + b).
La factorización de enteros en números primos se describe en el teorema fundamental de la aritmética y la factorización de polinomios (en ciertos contextos) en el teorema fundamental del álgebra.
En álgebra, la factorización es expresar un objeto o número (por ejemplo, un número compuesto, una matriz o un polinomio) como producto de otros objetos más pequeños (factores), (en el caso de números debemos utilizar los números primos) que, al multiplicarlos todos, resulta el objeto original. Por ejemplo, el número 15 se factoriza en números primos 3 × 5; y a²-b² se factoriza como binomio conjugados (a - b)(a + b).
La factorización de enteros en números primos se describe en el teorema fundamental de la aritmética y la factorización de polinomios (en ciertos contextos) en el teorema fundamental del álgebra.
Polinomios
En matemáticas, se denomina polinomio a la suma de varios monomios (llamados términos del polinomio). Es una expresión algebraica sobre un anillo conmutativo A constituida por un número finito de variables y constantes, utilizando solamente en operaciones de adición, sustracción, multiplicación y potenciación con exponentes de números naturales (es decir, usando sólo las operaciones internas del anillo
.
Por ejemplo:
El polinomio de un sólo término se denomina monomio; el de dos, binomio; el de tres, trinomio; el de cuatro, tetranomio. Cada uno de ellos y de los de mayor número de términos se llama polinomio de "N" términos, siendo "N" el número de términos de que se componga.
La expresión general de los polinomios que sólo tienen una variable, los más utilizados, es:
En matemáticas, se denomina polinomio a la suma de varios monomios (llamados términos del polinomio). Es una expresión algebraica sobre un anillo conmutativo A constituida por un número finito de variables y constantes, utilizando solamente en operaciones de adición, sustracción, multiplicación y potenciación con exponentes de números naturales (es decir, usando sólo las operaciones internas del anillo
.Por ejemplo:
es un polinomio, sin embargo:
no lo son, porque el primero involucra un exponente fraccionario y el segundo divisiones en la variable (una división entre la variable puede interpretarse como una potencia negativa en la variable).
El polinomio de un sólo término se denomina monomio; el de dos, binomio; el de tres, trinomio; el de cuatro, tetranomio. Cada uno de ellos y de los de mayor número de términos se llama polinomio de "N" términos, siendo "N" el número de términos de que se componga.
La expresión general de los polinomios que sólo tienen una variable, los más utilizados, es:
Suscribirse a:
Entradas (Atom)