Productos notables es el nombre que reciben aquellas multiplicaciones con expresiones algebraicas cuyo resultado puede ser escrito por simple inspección, sin verificar la multiplicación que cumplen ciertas reglas fijas. Su aplicación simplifica y sistematiza la resolución de muchas multiplicaciones habituales.
.
Factor común
El resultado de multiplicar un binomio a+b con un término c se obtiene aplicando la propiedad distributiva: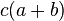 (el producto de la base por la altura), que también puede obtenerse como la suma de las dos áreas coloreadas (ca) y (cb).
(el producto de la base por la altura), que también puede obtenerse como la suma de las dos áreas coloreadas (ca) y (cb).
- Ejemplo

Binomio al cuadrado o cuadrado de un binomio
Para elevar un binomio al cuadrado (es decir, multiplicarlo por sí mismo), se suman los cuadrados de cada término con el doble del producto de ellos. Es decir: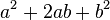 , se conoce como trinomio cuadrado perfecto.
, se conoce como trinomio cuadrado perfecto.Cuando el segundo término es negativo, la ecuación que se obtiene es:
- Ejemplo

Producto de dos binomios con un término común
Cuando se multiplican dos binomios que tienen un término común, se suma el cuadrado del término común con el producto el término común por la suma de los otros, y al resultado se añade el producto de los términos diferentes.- Ejemplo

Producto de dos binomios conjugados
Dos binomios conjugados son aquellos que sólo se diferencien en el signo de la operación. Para multiplicar binomios conjugados, basta elevar los monomios al cuadrado y restarlos, obteniendo una diferencia de cuadrados
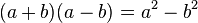
- Ejemplo

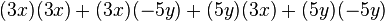
agrupando términos:
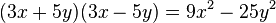
A este producto notable también se le conoce como suma por la diferencia
Polinomio al cuadrado
Para elevar un polinomio con cualquier cantidad de términos, se suman los cuadrados de cada término individual y luego se añade el doble de la suma de los productos de cada posible par de términos.

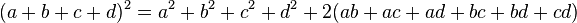
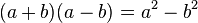

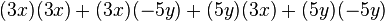
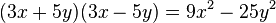

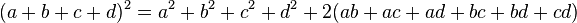
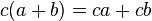
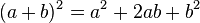
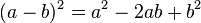
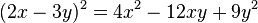
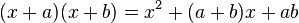
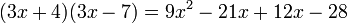

No hay comentarios:
Publicar un comentario